Advertisements
Advertisements
Question
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
Solution
Let us first put the given data in the form of a diagram.
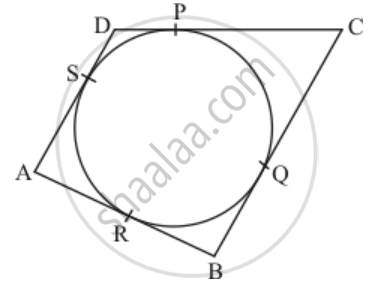
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
AR = SA
Let us represent AR and SA by ‘a’.
Similarly,
QB = RB
Let us represent SD and DP by ‘b’
PC = CQ
Let us represent PC and PQ by ‘c’
SD = DP
Let us represent QB and RB by ‘d’
It is given that,
AB = 4
AR + RB =4
a + b = 4
b = 4 − a …… (1)
Similarly,
BC = 5
That is,
b + c = 5
Let us substitute for b from equation (1). We get,
4 − a + c = 5
c − a = 1
c = a + 1 …… (2)
CD = 7
c + d = 7
Let us substitute for c from equation (2). We get,
a + 1 + d = 7
a + d = 6
In the previous section we had represented AS and SR with ‘a’ and SD and DP with ‘b’. We shall now put AS in place of ‘a’ and SD in place of ‘d’. We get,
AS + SD = 6
AD = 6 cm
Therefore, the length of the fourth side of the quadrilateral is 6 cm.
APPEARS IN
RELATED QUESTIONS
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
Find the area of a circle of radius 7 cm.
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
If the radius of a circle is 5 cm, what will its diameter be?
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.