Advertisements
Advertisements
Question
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
Options
15 cm
16 cm
17 cm
34 cm
Solution
17 cm
We will represent the given data in the figure
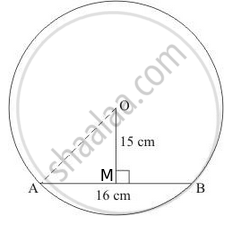
In the diagram AB is the given chord of 16 cm length and OM is the perpendicular distance from the centre to AB.
We know that perpendicular from the centre to any chord divides it into two equal parts.
So, AM = MB = `16/2` = 8 cm.
Now consider right triangle OMA and by using Pythagoras theorem
`AO^2 = AM^2 + OM^2`
`= 8^2 + 15^2`
= 64+225
= 289
`= sqrt(289)`
= 17 cm
APPEARS IN
RELATED QUESTIONS
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In the given figure, if ∠ABC = 45°, then ∠AOC =
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
