Advertisements
Advertisements
प्रश्न
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
पर्याय
15 cm
16 cm
17 cm
34 cm
उत्तर
17 cm
We will represent the given data in the figure
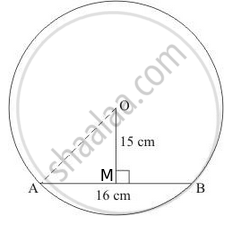
In the diagram AB is the given chord of 16 cm length and OM is the perpendicular distance from the centre to AB.
We know that perpendicular from the centre to any chord divides it into two equal parts.
So, AM = MB = `16/2` = 8 cm.
Now consider right triangle OMA and by using Pythagoras theorem
`AO^2 = AM^2 + OM^2`
`= 8^2 + 15^2`
= 64+225
= 289
`= sqrt(289)`
= 17 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Prove that there is one and only one tangent at any point on the circumference of a circle.
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
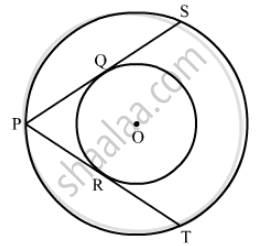
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Find the diameter of the circle
Radius = 10 cm
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.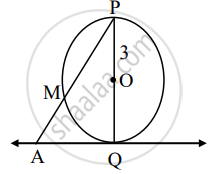
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.