Advertisements
Advertisements
Question
In the given figure, if ∠ABC = 45°, then ∠AOC =
Options
45°
60°
75°
90°
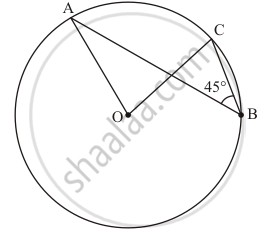
Solution
90°
We have to find ∠AOC.
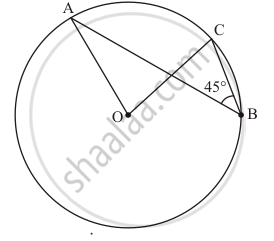
As we know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
`angleAOC = 2 angleABC`
`= 2 xx 45`
= 90°
APPEARS IN
RELATED QUESTIONS
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
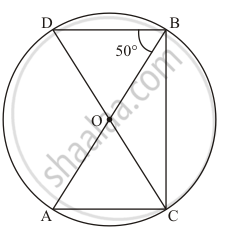
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

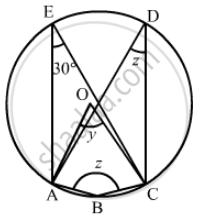
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.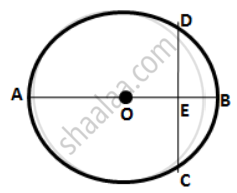
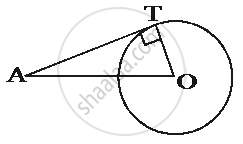
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
