Advertisements
Advertisements
Question
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
Options
2 : 3
1 : 4
4 : 1
1 : 3
Solution
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is 1 : 4.
Explanation:
An arc that subtends an angle of 90° at the center of a circle represents a quarter of the full circle because a full circle has 360°
`= (90°)/(360°) = 1/4`
Therefore, the ratio of the arc length to the circumference of the circle is 1 : 4
APPEARS IN
RELATED QUESTIONS
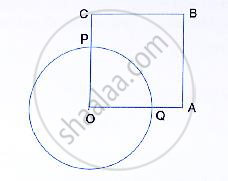
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
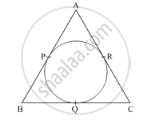
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
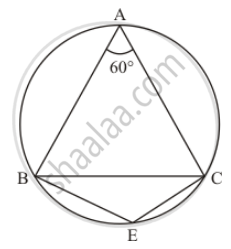
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
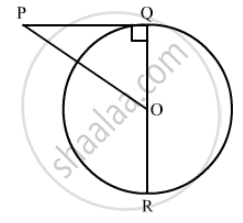
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.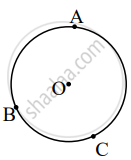
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

