Advertisements
Advertisements
Question
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
Options
60°
90°
120°
none of these
Solution
60°
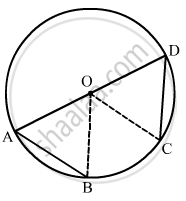
As we know that equal chords make equal angle at the centre.
Therefore,
\[\angle AOB = \angle BOC = \angle COD\]
\[\angle AOB + \angle BOC + \angle COD = 180° \left[ \text{ Linear pair } \right]\]
\[ \Rightarrow 3\angle AOB = 180°\]
\[ \Rightarrow \angle AOB = 60° \]
APPEARS IN
RELATED QUESTIONS
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

