Advertisements
Advertisements
Question
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
Options
3 cm
4 cm
5 cm
6 cm
Solution
6 cm
We are given a right triangle ABC such that `angleB ` = 90° , AC = 5 cm, AB = 4 cm. A circle is drawn with A as centre and AC as radius. We have to find the length of the chord of this circle passing through C and B. We have the following figure regarding the given information.
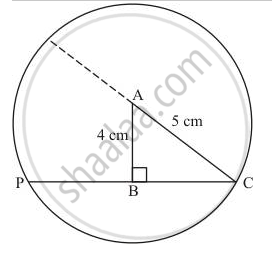
In the circle produce CB to P. Here PC is the required chord.
We know that perpendicular drawn from the centre to the chord divide the chord into two equal parts.
So, PC = 2BC
Now in ΔABC apply Pythagoras theorem
`BC^2 = AC^2 - AB^2`
`=5^2 - 4^2`
= 25 - 16
= 9
BC = 3 cm
So, PC = 2 × BC
= 2 × 3
= 6 cm
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
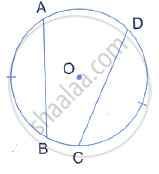
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

One chord of a circle is known to be 10 cm. The radius of this circle must be
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

