Advertisements
Advertisements
Question
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Solution
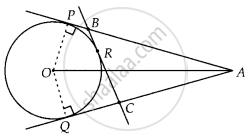
OP ⊥ AP
∴ ∠OPA = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
In ∆OAP,
OA2 = OP2 + PA2
⇒ 132 = 52 + PA2
⇒ PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AB + BR + RC + CA
= (AB + BR) + (RC + CA)
= (AB + BP) + (CQ + CA) ...[∵ BR = BP, RC = CQ i.e., tangents from external point to a circle are equal]
= AP + AQ
= 2AP ...[∵ AP = AQ]
= 2 × 12
= 24 cm
Hence, the perimeter of ∆ABC = 24 cm.
APPEARS IN
RELATED QUESTIONS
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
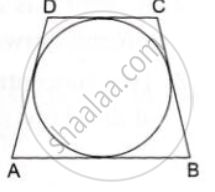
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

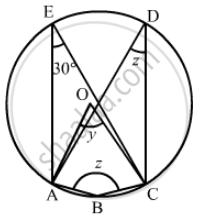
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
The greatest chord of a circle is called its
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
