Advertisements
Advertisements
Question
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
Solution
The angle between the tangent at the point of contact on a circle and the radius through the point is 90°.
APPEARS IN
RELATED QUESTIONS
In Fig., if AB = AC, prove that BE = EC
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
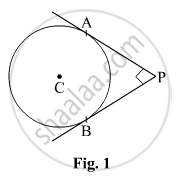
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
Draw circle with the radii given below.
4 cm
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure