Advertisements
Advertisements
प्रश्न
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

उत्तर
ΔAPB = 50°
By degree measure theorem
∠AOB=2 ∠APB
⇒∠APB= 2 × 50° = 100°
Since OA =OB
[ Radius of circle ]
Then ∠OAB=∠OBA
[ Angle's opposite to equal sides ]
Let ∠OAB = x
In Δ OAB by angle sum property
`∠OAB+∠OBA+∠AOB=180°`
`⇒x+x+100=180°`
`⇒2x+100=180°`
`⇒2x=80°`
`⇒x=40°`
`∠OAB =∠OBA= 40°`
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
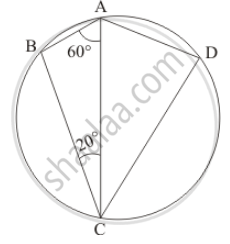
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
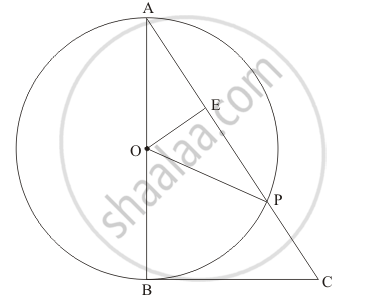
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
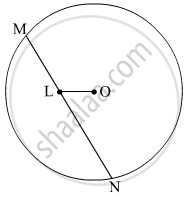
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
The longest chord of a circle is __________
A line through the point of contact and passing through centre of the circle is known as ______
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
