Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
рдЙрддреНрддрд░
BC = 6cm AB = 8cm
As ABC is right angled triangle
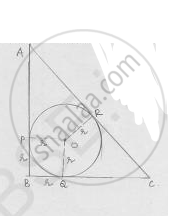
By Pythagoras theorem
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2 = 62 + 82 = 100
ЁЭР┤ЁЭР╢ = 10 ЁЭСРЁЭСЪ
Consider BQOP ∠B = 90°,
∠BPO = ∠OQB = 90° [At point of contact, radius is perpendicular to tangent]
All the angles = 90° & adjacent sides are equal
∴ BQOP is square BP = BQ = r
We know that
The tangents drawn from any external point are equal in length.
AP = AR = AB – PB = 8 – r
QC = RC = BC – BQ = 6 – r
AC = AR + RC ⇒ 10 = 8 – r + 6 – r
⇒ 10 = 14 – 2r
⇒ 2r = 4
⇒ Radius = 2cm
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
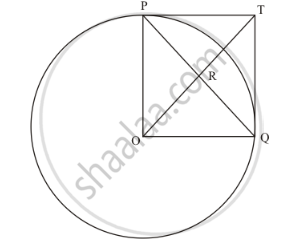
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
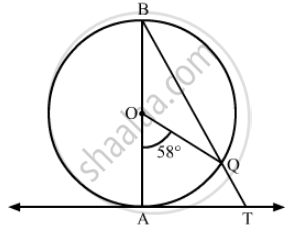
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
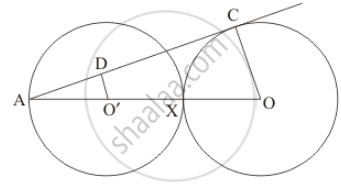
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.
