Advertisements
Advertisements
प्रश्न
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
उत्तर
BC = 6cm AB = 8cm
As ABC is right angled triangle
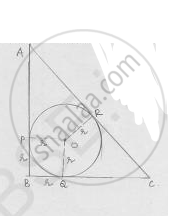
By Pythagoras theorem
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2 = 62 + 82 = 100
𝐴𝐶 = 10 𝑐𝑚
Consider BQOP ∠B = 90°,
∠BPO = ∠OQB = 90° [At point of contact, radius is perpendicular to tangent]
All the angles = 90° & adjacent sides are equal
∴ BQOP is square BP = BQ = r
We know that
The tangents drawn from any external point are equal in length.
AP = AR = AB – PB = 8 – r
QC = RC = BC – BQ = 6 – r
AC = AR + RC ⇒ 10 = 8 – r + 6 – r
⇒ 10 = 14 – 2r
⇒ 2r = 4
⇒ Radius = 2cm
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

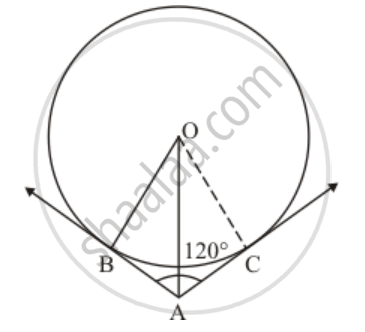
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
