Advertisements
Advertisements
प्रश्न
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
उत्तर
Radius of a circle = `4sqrt(2)` cm
In the right ΔAOC,

AC2 = OA2 + OC2
AC2 = `(4sqrt(2))^2 + (4sqrt(2))^2`
= 32 + 32 = 64
AC = `sqrt(64)`
= 8
Length of the chord = 8 cm,
∠OAC = ∠OCA = 45°
Since OAC is an isosceles right angle triangle.
APPEARS IN
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.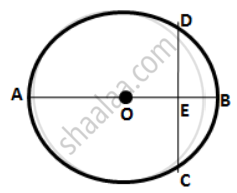
If O is the centre of the circle, find the value of x in each of the following figures

Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
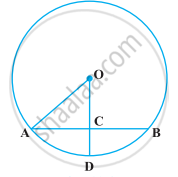
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

Is every chord of a circle also a diameter?
