Advertisements
Advertisements
प्रश्न
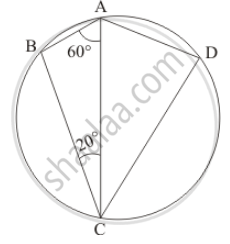
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
उत्तर
It is given that, `angle BAC = 60°` and `angle BCA = 20°`
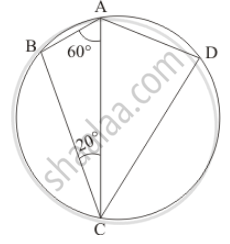
We have to find the `angle ADC `
In given Δ ABC we have
`angle ABC + angle BCA + angle BAC `= 180° \[ \left( \text{ Angle sum property } \right)\]
\[ \Rightarrow \angle ABC = 180° - \left( 60° + 20° \right) = 100° \]
In cyclic quadrilateral ABCD we have
`angle B + angleD = 180°` (Sum of pair of opposite angles of a cyclic quadilateral is 180º)
Then,
`angle D = 180° - 100° `
`angle D = 80° `
Hence `angle ADC = 80°`
APPEARS IN
संबंधित प्रश्न
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
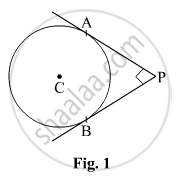
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

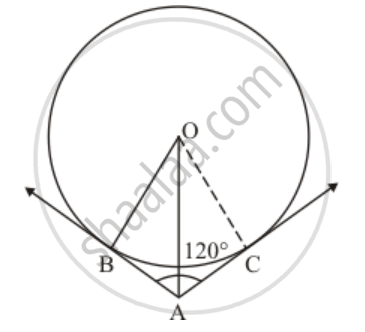
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Find the area of a circle of radius 7 cm.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Use the figure given below to fill in the blank:
Diameter = 2 x ________

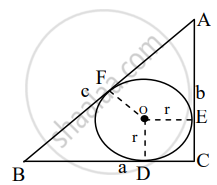
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c