Advertisements
Advertisements
प्रश्न
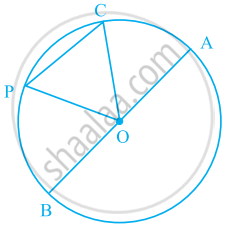
Use the figure given below to fill in the blank:
Diameter = 2 x ________

उत्तर
Diameter = 2 x radius.
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is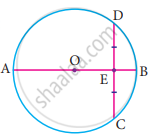
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
In the given figure, O is the centre of the circle. Name all radii of the circle.