Advertisements
Advertisements
प्रश्न
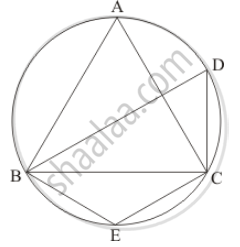
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
उत्तर
It is given that, ABC is an equilateral triangle
We have to find `angleBDC` and `angleBEC`
Since ΔABC is an equilateral triangle
So, `angleA = angleB = angleC = 60°`
And ABEC is cyclic quadrilateral
So `angle A + angle E = 180°` (Sum of opposite pair of angles of a cyclic quadrilateral is 180°.)
Then,
`angle E = 180° - 60°`
= 120°
Similarly BECD is also cyclic quadrilateral
So,
`angle E + angle D = 180°`
`angleD = 180° - 120°`
= 60°
Hence, `angle BDC `= 60° and `angle BEC = 120°`.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
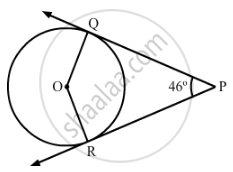
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
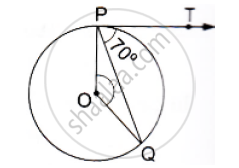
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
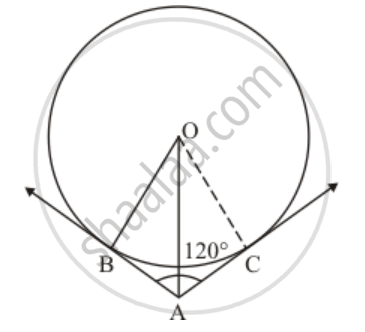
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
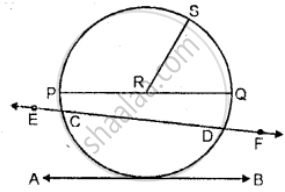
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

From the figure, identify a chord.

