Advertisements
Advertisements
प्रश्न
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
उत्तर
We know that the tangents drawn from any external point to circle are equal in length.
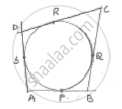
From A ⟶ AS = AP ….(i)
From B ⟶ QB = BP …. (ii)
From C ⟶ QC = RC …..(iii)
From D ⟶ DS = DR …. (iv)
Adding (i), (ii), (iii) & (iv)
(AS + QB + QC + DS) = (AB + BP + RC + OR)
(AS + DS) + (QB + QC) = (AP + BP) + (RC + DR)
AD + BC = AB + CD
⇒ AD + 7 = 6 + 4 AD = 3cm
⇒ AD = 10 – 7 = 3cm
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
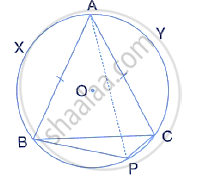
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
