Advertisements
Advertisements
प्रश्न
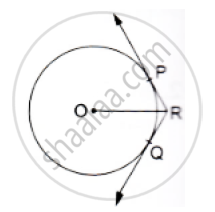
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
उत्तर

Radius of the circle, r = 10 cm
Area of sector OPRQ
`= 60^@/360^@ xx pir^2`
`= 1/6 xx 3.14 xx (10)^2`
`= 52.33 cm^3`
In ΔOPQ,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
So, area of ΔOPQ
`= sqrt3/4 xx ("Side")^2`
`= sqrt3/4 xx (10)^2`
`=( 100sqrt3)/4 cm^2`
=43.30 cm2
Area of minor segment PRQ
= Area of sector OPRQ − Area of ΔOPQ
= 52.33 − 43.30
= 9.03 cm2
Area of major segment PSQ
= Area of circle − Area of minor segment PRQ
=π(10)2 − 9.03
=314 − 9.03
= 304.97 cm2
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
The ratio between the circumference and diameter of any circle is _______
Find the diameter of the circle
Radius = 6 cm
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
