Advertisements
Advertisements
प्रश्न
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
उत्तर
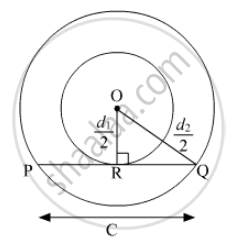
Let O be the centre of two concentric circles and PQ be the tangent to the inner circle that touches the circle at R.
Now, OQ= \[\frac{1}{2} d_2\] and
OR=\[\frac{1}{2} d_1\]
Also, PQ = c
As, PQ is the tangent to the circle.
⇒ OR ⊥ PQ
⇒ QR =\[\frac{1}{2}PQ = \frac{1}{2}c\]
In Triangle OQR,
∴ By Pythagoras Theorem,
\[\left( OQ \right)^2 = \left( OR \right)^2 + \left( RQ \right)^2 \]
\[ \Rightarrow \left( \frac{d_2}{2} \right)^2 = \left( \frac{d_1}{2} \right)^2 + \left( \frac{c}{2} \right)^2 \]
\[ \Rightarrow \left( d_2 \right)^2 = \left( d_1 \right)^2 + c^2\]
APPEARS IN
संबंधित प्रश्न
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
If O is the centre of the circle, find the value of x in each of the following figures

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
The length of tangent from an external point on a circle is always greater than the radius of the circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
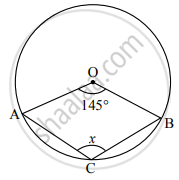
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.