Advertisements
Advertisements
प्रश्न
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

उत्तर

Given,
Radius, OP = 5 cm
PQ = 8 cm,
TP = TQ (Tangents drawn from a common point to a circle are equal)
Δ PTQ is isosceles.
Let PQ and OT intersect at point M.
TO is the angle bisector of ∠PTQ.
So, ∠PMT = 90° ⇒ PM = QM = 4 cm .... Perpendicular drawn from the center of the circle to the chord bisects the chord)
Given,
Radius, OP = 5 cm
PQ = 8 cm,
TP = TQ (Tangents drawn from a common point to a circle are equal)
Δ PTQ is isosceles.
Let PQ and OT intersect at point M.
TO is the angle bisector of ∠PTQ.
So, ∠PMT = 90° ⇒ PM = QM = 4 cm .... Perpendicular drawn from the center of the circle to the chord bisects the chord)
In Δ PMO,
OP2 = OM2 + PM2
⇒ 52 = OM2 + 42
⇒ OM = 3 cm
Let PT = x and TM = y
In Δ PMT,
PT2 = TM2 + PM2
x2 = y2 + 16 .....(i)
In Δ TPO,
OT2 = PT2 + OP2
(y + 3)2 = x2 + 52
y2 + 9 + 6y = x2 + 25 ....(ii)
From (i) and (ii), we get
y2 + 9 + 6y = y2 + 16 + 25
6y = 32
y = `16/3` cm
substituting y = `16/3`in equation (i),
`"x"^2 = (16/3)^2 + 16`
`x^2 = 400/9`
`x = 20/3` cm
Therefore, PT = `20/3` cm
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
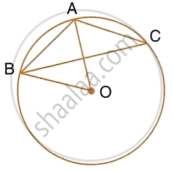
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
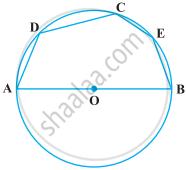
From the figure, identify three radii.