Advertisements
Advertisements
Question
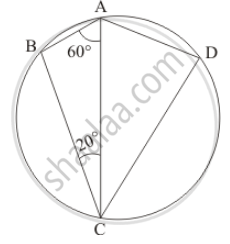
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
Solution
It is given that, `angle BAC = 60°` and `angle BCA = 20°`
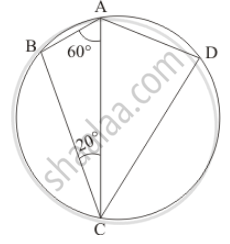
We have to find the `angle ADC `
In given Δ ABC we have
`angle ABC + angle BCA + angle BAC `= 180° \[ \left( \text{ Angle sum property } \right)\]
\[ \Rightarrow \angle ABC = 180° - \left( 60° + 20° \right) = 100° \]
In cyclic quadrilateral ABCD we have
`angle B + angleD = 180°` (Sum of pair of opposite angles of a cyclic quadilateral is 180º)
Then,
`angle D = 180° - 100° `
`angle D = 80° `
Hence `angle ADC = 80°`
APPEARS IN
RELATED QUESTIONS
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

Prove that two different circles cannot intersect each other at more than two points.
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.