Advertisements
Advertisements
Question
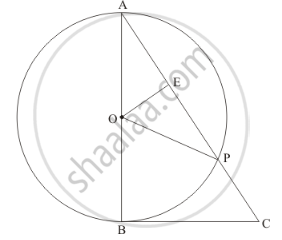
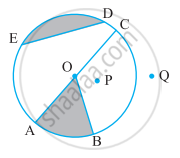
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.
Solution
The figure given in the question is below

Let us first take up ΔAOP.
We have,
OA = OP (Since they are the radii of the same circle)
Therefore, ΔAOP is an isosceles triangle. From the property of isosceles triangle,
we know that, when a median drawn to the unequal side of the triangle will be
perpendicular to the unequal side. Therefore,
∠OEA=90°
Now let us take up ΔAOE and ΔABC.
We know that the radius of the circle will always be perpendicular to the tangent at
the point of contact. In this problem, OB is the radius and BC is the tangent
and B is the point of contact. Therefore,
∠ABC=90°
Also, from the property of isosceles triangle we have found that
∠OEA=90°
Therefore,
∠ABC=∠OEA
∠A is the common angle to both the triangles.
Therefore, from AA postulate of similar triangles,
ΔAOE~ΔABC
Thus we have proved
RELATED QUESTIONS
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

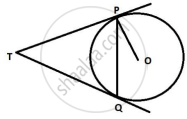
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Write True or False. Give reason for your answer.
A circle is a plane figure.
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
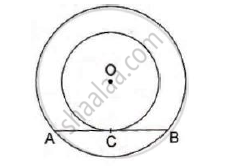
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
One chord of a circle is known to be 10 cm. The radius of this circle must be
The greatest chord of a circle is called its
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
In the given figure, if ∠ABC = 45°, then ∠AOC =
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

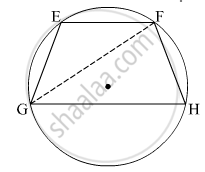
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.
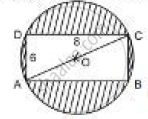
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
In the given circle with diameter AB, find the value of x.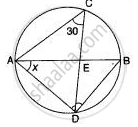
If O is the centre of the circle, find the value of x in each of the following figures

Use the figure given below to fill in the blank:
AB is a ______ of the circle.
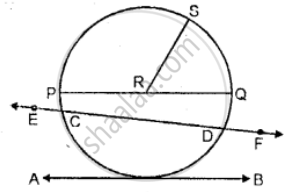
A line segment joining any point on the circle to its center is called the _____________ of the circle
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
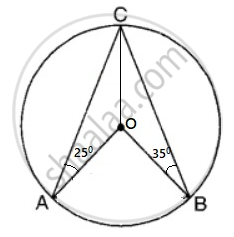
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
From the figure, identify a segment.
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
