Advertisements
Advertisements
प्रश्न
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
उत्तर १
Let D, E, F be the mid-points of the sides BC, CA and AB respectively. Then, the coordinates of D, E and F are
`D( \frac{5+3}{2},\ \frac{3-1}{2})=D(4,\text{ 1}),`
`E( \frac{3+7}{2},\ \frac{-1-3}{2})=E( 5,-2 )`
`F((7+5)/2,(3-(-3))/2)=F(6,3)`
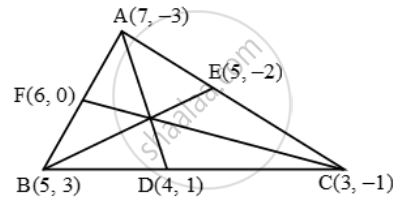
`\therefore AD=sqrt((7-4)^{2}+(-3-1)^{2})=\sqrt{9+16}=5`
`BE=sqrt((5-5)^{2}+(-2-3)^{2})=sqrt{0+25}=5`
`CF=sqrt((6-3)^{2}+(3-(-1))^{2})=sqrt{9+16}=5`
the lengths of the medians is 5
उत्तर २
The given vertices are A(7, –3), B(5,3) and C(3,–1).
Since D and E are the midpoints of BC and AC respectively. therefore
`"Coordinates of " D = ((5+3)/2 , (3-1)/2) = (4,1)`
`" Coordinates of " E = ((7+3)/2 , (-3-1)/2) = (5,-2)`
Now ,
`AD = sqrt((7-4)^2 +(-3-1)^2) = sqrt(9+16)=5`
`BE = sqrt((5-5)^2 +(3+2)^2) = sqrt(0+25) = 5`
Hence, AD = BE = 5 units.
APPEARS IN
संबंधित प्रश्न
Find the length of the medians of a ΔABC having vertices at A(0, -1), B(2, 1) and C(0, 3).
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
AB is a diameter of a circle with centre C = (–2, 5). If A = (3, –7), find
- the length of radius AC.
- the coordinates of B.
Find the coordinates of the points of trisection of the line segment joining the points (3, -3) and ( 6, 9).
The points A, B and C divides the line segment MN in four equal parts. The coordinates of Mand N are (-1, 10) and (7, -2) respectively. Find the coordinates of A, B and C.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.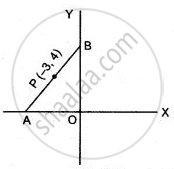
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
Find the ratio in which the line segment joining the points A(6, 3) and B(–2, –5) is divided by x-axis.
