Question

Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)

Answer 1

Let D, E, F be the mid-points of the sides BC, CA and AB respectively. Then, the coordinates of D, E and F are

${\displaystyle D(\frac{5+3}{2}, \frac{3-1}{2})=D(4,\text{1}),}$

${\displaystyle E(\frac{3+7}{2}, \frac{-1-3}{2})=E(5,-2)}$

${\displaystyle F(\frac{7+5}{2},\frac{3-(-3)}{2})=F(6,3)}$

${\displaystyle \therefore AD=\sqrt{{(7-4)}^2+{(-3-1)}^2}=\sqrt{9+16}=5}$

${\displaystyle BE=\sqrt{{(5-5)}^2+{(-2-3)}^2}=\sqrt{0+25}=5}$

${\displaystyle CF=\sqrt{{(6-3)}^2+{(3-(-1))}^2}=\sqrt{9+16}=5}$

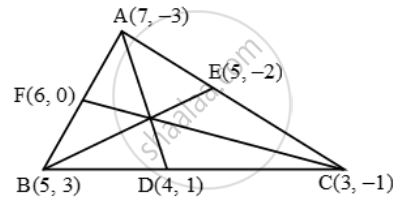
 the lengths of the medians is 5

Answer 2

The given vertices are A(7, –3), B(5,3) and C(3,–1).

Since D and E are the midpoints of BC and AC respectively. therefore

${\displaystyle \text{Coordinates of}D=(\frac{5+3}{2},\frac{3-1}{2})=(4,1)}$

${\displaystyle \text{Coordinates of}E=(\frac{7+3}{2},\frac{-3-1}{2})=(5,-2)}$

Now , 

${\displaystyle AD=\sqrt{{(7-4)}^2+{(-3-1)}^2}=\sqrt{9+16}=5}$

${\displaystyle BE=\sqrt{{(5-5)}^2+{(3+2)}^2}=\sqrt{0+25}=5}$

Hence, AD = BE = 5 units.