Advertisements
Advertisements
Question
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
Solution 1
Let D, E, F be the mid-points of the sides BC, CA and AB respectively. Then, the coordinates of D, E and F are
`D( \frac{5+3}{2},\ \frac{3-1}{2})=D(4,\text{ 1}),`
`E( \frac{3+7}{2},\ \frac{-1-3}{2})=E( 5,-2 )`
`F((7+5)/2,(3-(-3))/2)=F(6,3)`
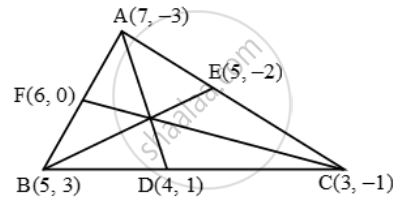
`\therefore AD=sqrt((7-4)^{2}+(-3-1)^{2})=\sqrt{9+16}=5`
`BE=sqrt((5-5)^{2}+(-2-3)^{2})=sqrt{0+25}=5`
`CF=sqrt((6-3)^{2}+(3-(-1))^{2})=sqrt{9+16}=5`
the lengths of the medians is 5
Solution 2
The given vertices are A(7, –3), B(5,3) and C(3,–1).
Since D and E are the midpoints of BC and AC respectively. therefore
`"Coordinates of " D = ((5+3)/2 , (3-1)/2) = (4,1)`
`" Coordinates of " E = ((7+3)/2 , (-3-1)/2) = (5,-2)`
Now ,
`AD = sqrt((7-4)^2 +(-3-1)^2) = sqrt(9+16)=5`
`BE = sqrt((5-5)^2 +(3+2)^2) = sqrt(0+25) = 5`
Hence, AD = BE = 5 units.
APPEARS IN
RELATED QUESTIONS
Determine the ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7)
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
A line segment joining A`(-1,5/3)` and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis.
- Calculate the value of ‘a’.
- Calculate the co-ordinates of ‘P’.
Find the coordinate of a point P which divides the line segment joining :
A (3, -3) and B (6, 9) in the ratio 1 :2.
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
Using section formula, show that the points A(7, −5), B(9, −3) and C(13, 1) are collinear
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
Find the ratio in which the line segment joining the points A(6, 3) and B(–2, –5) is divided by x-axis.
Read the following passage:
Jagdish has a field which is in the shape of a right angled triangle AQC. He wants to leave a space in the form of a square PQRS inside the field for growing wheat and the remaining for growing vegetables (as shown in the figure). In the field, there is a pole marked as O. |
Based on the above information, answer the following questions :
- Taking O as origin, coordinates of P are (–200, 0) and of Q are (200, 0). PQRS being a square, what are the coordinates of R and S?
- (a) What is the area of square PQRS?
OR
(b) What is the length of diagonal PR in square PQRS? - If S divides CA in the ratio K : 1, what is the value of K, where point A is (200, 800)?
