Advertisements
Advertisements
Question
Using section formula, show that the points A(7, −5), B(9, −3) and C(13, 1) are collinear
Solution
If three points are collinear, then one of the points divide the line segment joining the other points in the ratio r : 1. If P is between A and B and `"AP"/"PB"` = r
Distance AB = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
= `sqrt((9 - 7)^2 + (-3 + 5)^2`
= `sqrt(2^2 + 2^2)`
= `sqrt(4 + 4)`
= `sqrt(8)`
= `2sqrt(2)`
Distance BC = `sqrt((13 - 9)^2 + (1 + 3)^2`
= `sqrt(4^2 + 4^2)`
= `sqrt(16 + 16)`
= `sqrt(32)`
= `sqrt(16 xx 2)`
= `4sqrt(2)`
To find r
r = `"AB"/"BC" = (2sqrt(2))/(4sqrt(2))`
`"AB"/"BC" = 1/2`
The line divides in the ratio 1 : 2
A line divides internally in the ratio m : n
The point P = `(("m"x_2 + "n"x_1)/("m" + "n"), ("m"y_2 + "n"y_1)/("m" + "n"))`
m = 1, n = 2, x1 = 7, x2 = 13, y1 = – 5, y2 = 1
By the given equation,
The point B = `((13 + 14)/5, (1 - 10)/3)`
= `(27/3, (-9)/3)`
= (9, −3)
∴ The three points A, B and C are collinear.
APPEARS IN
RELATED QUESTIONS
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
If A and B are two points having coordinates (−2, −2) and (2, −4) respectively, find the coordinates of P such that `AP = 3/7 AB`
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
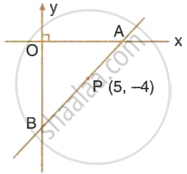
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
Find the coordinates of point P which divides line segment joining A ( 3, -10) and B (3, 2) in such a way that PB: AB= 1.5.
A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively ______.
In what ratio does the x-axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
If A and B are (– 2, – 2) and (2, – 4) respectively; then find the co-ordinates of the point P such that `(AB)/(AB) = 3/7`.
