Advertisements
Advertisements
Question
In what ratio does the x-axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
Solution
Let the ratio in which x-axis divides the line segment joining (– 4, – 6) and (–1, 7) = 1 : k
Then,
x-coordinate becomes `(-1 - 4k)/(k + 1)`
y-coordinate becomes `(7 - 6k)/(k + 1)`
Since P lies on x-axis, y coordinate = 0
`(7 - 6k)/(k + 1)` = 0
7 – 6k = 0
k = `6/7`
Now, m1 = 6 and m2 = 7
By using section formula,
x = `(m_1x_2 + m_2x_1)/(m_1 + m_2)`
= `(6(-1) + 7(-4))/(6 + 7)`
= `(-6 - 28)/13`
= `(-34)/13`
So, now
y = `(6(7) + 7(-6))/(6 + 7)`
= `(42 - 42)/13`
= 0
Hence, the coordinates of P are `((-34)/13, 0)`
APPEARS IN
RELATED QUESTIONS
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
In what ratio does the point `(24/11, y)` divide the line segment joining the points P(2, –2) and Q(3, 7)? Also find the value of y.
If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0 find the value of k.
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that `(AP)/(PB) = k/1`. If P lies on the line x + y = 0, then find the value of k.
If A = (−4, 3) and B = (8, −6)
- Find the length of AB.
- In what ratio is the line joining A and B, divided by the x-axis?
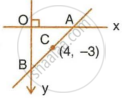
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Find the coordinate of a point P which divides the line segment joining :
D(-7, 9) and E( 15, -2) in the ratio 4:7.
In what ratio does the point (1, a) divided the join of (−1, 4) and (4, −1) Also, find the value of a.
If the points A(1, –2), B(2, 3) C(a, 2) and D(– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.
