Advertisements
Advertisements
Question
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
Solution
i. Co-ordinates of point P are
`((1 xx 17 + 2 xx (-4))/(1 + 2),(1 xx 10 + 2 xx 1)/(1 + 2))`
= `((17 - 8)/3, (10 + 2)/3)`
= `(9/3, 12/3)`
= (3, 4)
ii. `OP = sqrt((0 - 3)^2 + (0 - 4)^2)`
`OP = sqrt(9 + 16)`
`OP = sqrt(25)`
OP = 5 units
iii. Let AB be divided by the point P(0, y) lying on y-axis in the ratio k : 1
∴ `(0, y) = ((k xx 17 + 1 xx (-4))/(k + 1),(k xx 10 + 1 xx 1)/(k + 1))`
`=> (0, y) = ((17k - 4)/(k + 1),(10k + 1)/(k + 1))`
`=> 0 = (17k - 4)/(k + 1)`
`=> 17k - 4 = 0`
`=> k = 4/17`
Thus, the ratio in which the y-axis divide the line AB is 4 : 17.
APPEARS IN
RELATED QUESTIONS
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, -3) and B is (1, 4).
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the ratio in which the line segment joining P ( 4, -6) and Q ( -3, 8) is divided by the line y = 0.
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.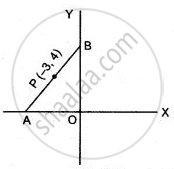
The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at ______.
If the points A(1, 2), O(0, 0), C(a, b) are collinear, then ______.
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
If the points A(2, 3), B(–5, 6), C(6, 7) and D(p, 4) are the vertices of a parallelogram ABCD, find the value of p.
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
