Advertisements
Advertisements
Questions
Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, -3) and B is (1, 4).
Find the coordinates of a point A, where AB is a diameter of a circle with center C (2, -3) and the other end of the diameter is B (1, 4).
Solution 1
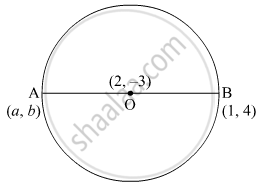
Let the centre of the circle be O.
Since AB is the diameter so, O is the midpoint of AB.
Thus, using the section formula,
`("a" +1)/2 = 2`
⇒ a = 4 - 1
⇒ a = 3
and
`("b" + 4)/2 = -3`
⇒ b = -10
So, the coordinate of point A is (3, -10).
Solution 2
C (2, -3) is the center of the given circle. Let A(a, b) and B(1, 4) be the two end-points of the given diameter AB. Then, the coordinates of C are
`x = (a+1)/2 , y =( b+4)/2`
It is given that x = 2 and y = -3
⇒ `2= (a+1)/2, 3 = (b+4)/2`
⇒ 4 = a + 1, -6 = b + 4
⇒ a = 4 - 1, b = -6 - 4
⇒ a = 3, b = -10
Therefore, the coordinates of point A are (3, -10).
APPEARS IN
RELATED QUESTIONS
Two vertices of a triangle are (3, –5) and (–7, 4). If its centroid is (2, –1). Find the third vertex
Find the lengths of the medians of a triangle whose vertices are A (−1,3), B(1,−1) and C(5, 1).
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that `(AP)/(PB) = k/1`. If P lies on the line x + y = 0, then find the value of k.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
Find the ratio in which the join of (–4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
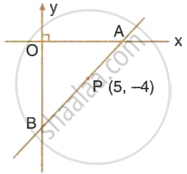
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.
Find the ratio in which the y-axis divides the line segment joining the points (−4, − 6) and (10, 12). Also find the coordinates of the point of division ?
In Figure 2, P (5, −3) and Q (3, y) are the points of trisection of the line segment joining A (7, −2) and B (1, −5). Then y equals

Find the coordinate of a point P which divides the line segment joining :
A (3, -3) and B (6, 9) in the ratio 1 :2.
Find the coordinate of a point P which divides the line segment joining :
D(-7, 9) and E( 15, -2) in the ratio 4:7.
Find the points of trisection of the segment joining A ( -3, 7) and B (3, -2).
The fourth vertex D of a parallelogram ABCD, whose three vertices are A(–2, 3), B(6, 7) and C(8, 3), is ______.
Find the ratio in which the point `P(3/4, 5/12)` divides the line segment joining the points `A(1/2, 3/2)` and B(2, –5).
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
