Advertisements
Advertisements
Question
A (2, 5), B (-1, 2) and C (5, 8) are the vertices of triangle ABC. Point P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2. Calculate the coordinates of P and Q. Also, show that 3PQ = BC.
Solution
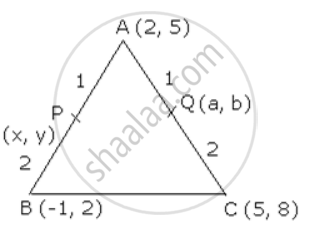
AP : PB = 1 : 2
Coordinates of P are,
P (x , y) = P `((-1 + 4)/(2 + 1) , (10 + 2)/(2 + 1)) = "P" (1 , 4)`
AQ : QC = 1 : 2
Coordinates of Q are,
Q (a , b) = Q `((4 + 5)/(2 + 1) , (10+ 8)/(2 + 1))` = Q (3 , 6)
Coordinates of P and Q are ( 1, 4) and (3, 6)
PQ = `sqrt ((3 - 1)^2 + (6 - 4)^2) = sqrt (4 + 4) = 2 sqrt 2` units
BC = `sqrt ((5 +1)^2 + (8 - 2)^2) = sqrt (36 + 36) = 6 sqrt 2` units
Hence proved, 3PQ = BC
APPEARS IN
RELATED QUESTIONS
Find the coordinates of the points which divide the line segment joining A (−2, 2) and B (2, 8) into four equal parts.
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
AB is a diameter of a circle with centre C = (–2, 5). If A = (3, –7), find
- the length of radius AC.
- the coordinates of B.
The line joining P (-5, 6) and Q (3, 2) intersects the y-axis at R. PM and QN are perpendiculars from P and Q on the x-axis. Find the ratio PR: RQ.
Find the points of trisection of the segment joining A ( -3, 7) and B (3, -2).
Show that the lines x = O and y = O trisect the line segment formed by joining the points (-10, -4) and (5, 8). Find the points of trisection.
Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).
