Advertisements
Advertisements
प्रश्न
Find the coordinates of the points of trisection of the line segment joining the points (3, -3) and ( 6, 9).
उत्तर

Let A (x, y) and B (a, b) be the points of trisection of line segment MN MA:.AN=1 :2
∴ cocrdinates of A are,
x = `(1 xx 6 + 2 xx 3)/(1 + 2) = 4`
y = `(1 xx 9 + 2 xx -3)/(1 +2) = 1`
A (4 , 1)
Also, MB : BN = 2 : 1
coordinates of B are,
a = `(2 xx 6 + 1 xx 3)/(2 + 1) = 5`
b = `(2 xx 9 + 1 xx -3)/(2 1) = 5`
B (5 , 5)
points of trisection are ( 4, 1) and (5, 5).
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 : 2 internally.
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
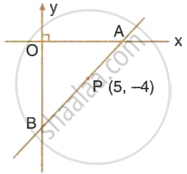
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
Find the co-ordinates of the points of tri-section of the line joining the points (–3, 0) and (6, 6).
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Find the length of the hypotenuse of a square whose side is 16 cm.
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
Find the ratio In which is the segment joining the points (1, - 3} and (4, 5) ls divided by x-axis? Also, find the coordinates of this point on the x-axis.
The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at ______.
