Advertisements
Advertisements
प्रश्न
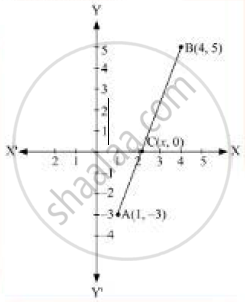
Find the ratio In which is the segment joining the points (1, - 3} and (4, 5) ls divided by x-axis? Also, find the coordinates of this point on the x-axis.
उत्तर
let C( x, 0) divides the Line segment joining the points A(1, - 3) and B(4,5) in k:1 ratio, By section formula,
(x, y)=`((mx_2 +nx_1)/(m+n) ,(my_2+ny_1)/(m+n))`
lmplies that
(x, 0)=` (( 4k +1 xx 1)/( k +1 ), (5k+1 xx (-3))/( k +1))`
Implies that
(x,0)= `((4k +1)/( k +1 ),(5k-3)/(k +1 ))`
Implies that
`(5k - 3)/(k +1 )= 0`
Implies that
5k - 3 = 0
Implies that
5k =3
`k = 3/5`
and x `=(4k+1)/(k+1) = (4 xx 3/5 +1)/(3/5+1) `
⇒ x = `((12+5)/5)/((3+5)/5)`
⇒ x = `17/8`
Therefore , coordinates of point P are `(17/8,0)`.
APPEARS IN
संबंधित प्रश्न
In what ratio does the x-axis divide the line segment joining the points (2, –3) and (5, 6)? Also, find the coordinates of the point of intersection.
If A(–2, –1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b
Prove that the diagonals of a rectangle bisect each other and are equal.
In what ratio does the point (1, a) divided the join of (−1, 4) and (4, −1) Also, find the value of a.
The origin o (0, O), P (-6, 9) and Q (12, -3) are vertices of triangle OPQ. Point M divides OP in the ratio 1: 2 and point N divides OQ in the ratio 1: 2. Find the coordinates of points M and N. Also, show that 3MN = PQ.
If the points A(1, 2), O(0, 0), C(a, b) are collinear, then ______.
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
Point C divides the line segment whose points are A(4, –6) and B(5, 9) in the ratio 2:1. Find the coordinates of C.
Find the co-ordinates of the points of trisection of the line segment joining the points (5, 3) and (4, 5).
