Question

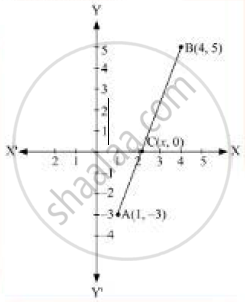
Find the ratio In which is the segment joining the points (1, - 3} and (4, 5) ls divided by x-axis?  Also, find the coordinates of this point on the x-axis.

Answer 1

let C( x, 0) divides the Line segment joining the points A(1, - 3) and B(4,5) in k:1 ratio, By section formula,

(x, y)=`((mx_2 +nx_1)/(m+n) ,(my_2+ny_1)/(m+n))`
lmplies that
(x, 0)=` (( 4k +1 xx 1)/( k +1 ), (5k+1 xx (-3))/( k +1))`
Implies that
(x,0)= `((4k +1)/( k +1 ),(5k-3)/(k +1 ))`
Implies that
`(5k - 3)/(k +1 )= 0`

Implies that
5k - 3 = 0

Implies that
5k =3
`k = 3/5`
and x `=(4k+1)/(k+1) = (4 xx 3/5 +1)/(3/5+1) `

⇒ x = `((12+5)/5)/((3+5)/5)`

⇒ x = `17/8`
Therefore , coordinates of point P are `(17/8,0)`.