Question

In what ratio is the join of (4, 3) and (2, –6) divided by the x-axis? Also, find the co-ordinates of the point of intersection.

Answer 1

Let P(x, 0) be the point of intersection which divides the line joining the points A(4, 3), B(2, –6) in the ratio of m₁ : m₂ 

∴ `x = (m_1 xx 2 + m_2 xx 4)/(m_1 + m_2)`

= `(2m_1 + 4m_2)/(m_1 + m_2)`  ....(i)

And `0 = (m_1 xx (-6) + m_2(3))/(m_1 + m_2)`

`\implies` – 6m₁ + 3m₂ = 0

`\implies` 3m₂ = 6m₁

`\implies m_1/m_2 = 3/6 = 1/2`

∴ Required ratio be m₁ : m₂ = 1 : 2

Now, substituting the value of m₁ and m₂ in (i); we have

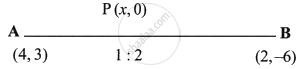
`x = (1 xx 2 + 2 xx 4)/(1 + 2)`

= `(2 + 8)/3`

= `10/3`

∴ Required point of intersection is `(10/3, 0)`