Question

The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at ______.

पर्याय

• (0, 13)

• (0, –13)

• (0, 12)

• (13, 0)

Answer 1

The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at (0, 13).

Explanation:

Firstly, we plot the points of the line segment on the paper and join them.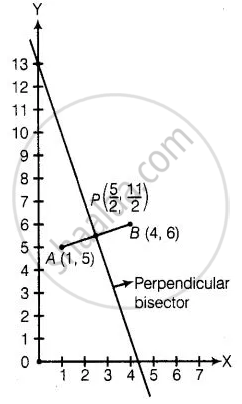

We know that, the perpendicular bisector of the line segment AB bisect the segment AB, i.e., perpendicular bisector of line segment AB passes through the mid-point of AB.

∴ Mid-point of AB = `((1 + 4)/2, (5 + 6)/2)`    ...`[∵ "Mid-point of line segment passes through the points"  (x_1, y_1)  "and"  (x_2, y_2) = ((x_1 + x_2)/2, (y_1 + y_2)/2)]`

⇒ P = `(5/2, 11/2)`

Now, we draw a straight line on paper passes through the mid-point P.

We see that the perpendicular bisector cuts the Y-axis at the point (0, 13).

Hence, the required point is (0, 13).

Answer 2

The perpendicular bisector of the line segment joining the points A(1, 5) and B(4, 6) cuts the y-axis at (0, 13).

Explanation:

We know that, the equation of line which passes through the points (x₁, y₁) and (x₂, y₂) is

`(y - y_1) = (y_2 - y_1)/(x_2 - x_1) (x - x_1)`  ...(i)

Here, x₁ = 1, y₁ = 5 and x₂ = 4, y₂ = 6

So, the equation of line segment joining the points A(1, 5) and B(4, 6) is 

`(y - 5) = (6 - 5)/(4 - 1)(x - 1)`

⇒ `(y - 5) = 1/3(x - 1)`

⇒ `3y - 15 = x - 1`

⇒ `3y = x - 14`

⇒ `y = 1/3x - 14/3`  ...(ii)

∴ Slope of the line segment, m₁ = `1/3`

If two lines are perpendicular to each other, then the relation between its slopes is 

m₁ · m₂ = – 1  ...(iii)

Where, m₁ = Slope of line 1

And m₂ = Slope of line 2

Also, we know that the perpendicular bisector of the line segment is perpendicular on the line segment.

Let slope of line segment is m₂.

From equation (iii),

`m_1 * m_2 = 1/3 * m_2` = – 1

⇒ m₂ = – 3

Also we know that the perpendicular bisector is passes through the mid-point of line segment.

∴ Mid-point of line segment = `((1 + 4)/2, (5 + 6)/2) = (5/2, 11/2)`

Equation of perpendicular bisector, which has slope (–3) and passes through the point `(5/2, 11/2)` is 

`(y - 11/2) = (-3)(x - 5/2)`   ...[Since, equation of line passes through the point (x₁, y₁) and having slope m(y – y₁) = m(x – x₁)]

⇒ (2y – 11) = – 3(2x – 5)

⇒ 2y – 11 = – 6x + 15

⇒ 6x + 2y = 26

⇒ 3x + y = 13  ...(iv)

If the perpendicular bisetor cuts the Y-axis,

Then put x = 0 in equation (iv),

3 × 0 + y = 13

⇒ y = 13

So, the required point is (0, 13).