Advertisements
Advertisements
प्रश्न
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.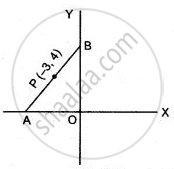
उत्तर
AP : PB = 2 : 3
Let A(x, 0) and B(0, y)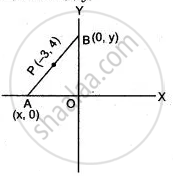
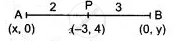
∴ By section formula
`(2 xx 0 + 3 xx x)/(2 + 3)` = -3
⇒ 3x = -15
x = -5
and `(2 xx y + 3 xx 0)/(2 + 3)` = 4
⇒ 2y = 20
⇒ y = 10
∴ Coordinates of A = (x, 0) = (-5, 0)
and B = (0, y) = (0, 10).
APPEARS IN
संबंधित प्रश्न
Two vertices of a triangle are (3, –5) and (–7, 4). If its centroid is (2, –1). Find the third vertex
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
A (2, 5), B (–1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP : PB = AQ : QC = 1 : 2.
- Calculate the co-ordinates of P and Q.
- Show that : `PQ = 1/3 BC`.
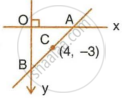
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the line y = O ?
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
If point P(1, 1) divide segment joining point A and point B(–1, –1) in the ratio 5 : 2, then the coordinates of A are ______
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
