Advertisements
Advertisements
Question
The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:
- the ratio PR : RQ
- the coordinates of R.
- the area of the quadrilateral PMNQ.
Solution
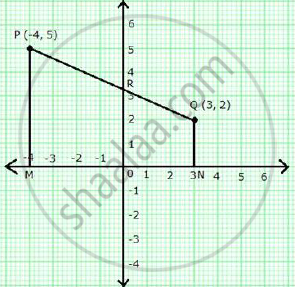
i. Let point R (0, y) divides PQ in the ratio k : 1.
We have:
`x = (k xx 3 + 1 xx (-4))/(k + 1)`
`0 = (3k - 4)/(k + 1)`
`0 = 3k - 4`
`k = 4/3`
Thus, PR : RQ = 4 : 3
ii. Also, we have:
`y = (k xx 2 + 1 xx 5)/(k + 1)`
`y = (2k + 5)/(k + 1)`
`y = (2 xx 4/3 + 5)/(4/3 + 1)`
`y = (8 + 15)/(4 + 3)`
`y = 23/7`
Thus, the co-ordinates of point R are `(0, 23/7)`
iii. Area of quadrilateral PMNQ
= `1/2 xx (PM + QN) xx MN`
= `1/2 xx (5 + 2) xx 7`
= `1/2 xx 7 xx 7`
= 24.5 sq. units
APPEARS IN
RELATED QUESTIONS
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, −3). Also, find the value of x.
Prove that (4, – 1), (6, 0), (7, 2) and (5, 1) are the vertices of a rhombus. Is it a square?
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
In what ratio is the line joining A(0, 3) and B(4, –1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
A line intersects y-axis and x-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, them find the coordinates of P and Q.
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
