Advertisements
Advertisements
Question
Find the ratio in which the point P(x, 2) divides the line segment joining the points A(12, 5) and B(4, −3). Also, find the value of x.
Solution 1
Let the point P (x, 2) divide the line segment joining the points A (12, 5) and B (4, −3) in the ratio k:1.
Then, the coordinates of P are `((4k+12)/(k+1),(-3k+5)/(k+1))`
Now, the coordinates of P are (x, 2).
`therefore (4k+12)/(k+1)=x and (-3k+5)/(k+1)=2`
`(-3k+5)/(k+1)=2`
`-3k+5=2k+2`
`5k=3`
`k=3/5`
Substituting `k=3/5 " in" (4k+12)/(k+1)=x`
we get
`x=(4xx3/5+12)/(3/5+1)`
`x=(12+60)/(3+5)`
`x=72/8`
x=9
Thus, the value of x is 9.
Also, the point P divides the line segment joining the points A(12, 5) and (4, −3) in the ratio 3/5:1 i.e. 3:5.
Solution 2
Let k be the ratio in which the point P(x,2) divides the line joining the points
`A(x_1 =12, y_1=5) and B(x_2 = 4, y_2 = -3 ) .` Then
`x= (kxx4+12)/(k+1) and 2 = (kxx (-3)+5) /(k+1)`
Now,
` 2 = (kxx (-3)+5)/(k+1) ⇒ 2k+2 = -3k +5 ⇒ k=3/5`
Hence, the required ratio is3:5 .
APPEARS IN
RELATED QUESTIONS
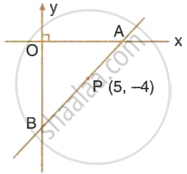
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
Show that A (3, –2) is a point of trisection of the line segment joining the points (2, 1) and (5, −8). Also, find the co-ordinates of the other point of trisection.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
Find the coordinates of a point P, which lies on the line segment joining the points A (−2, −2), and B (2, −4), such that `AP=3/7 AB`.
B is a point on the line segment AC. The coordinates of A and B are (2, 5) and (1, 0). If AC= 3 AB, find the coordinates of C.
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is ______.
In what ratio does the x-axis divide the line segment joining the points (– 4, – 6) and (–1, 7)? Find the coordinates of the point of division.
In what ratio does the Y-axis divide the line segment P(– 3, 1) and Q(6, 2)?
