Advertisements
Advertisements
प्रश्न
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
उत्तर
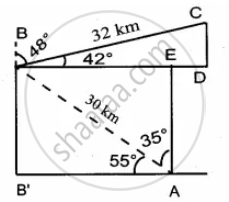
To find the distance of B to the north of A
In ∆ABB',
cos 55° = `"AB'"/"AB"`
0.5736 = `"AB'"/30`
Distance of B to the North of A = 24.58 km
APPEARS IN
संबंधित प्रश्न
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5m from the banks, find the width of the river.
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
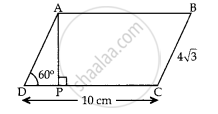
In given figure, ABCD is a || gm. The length of AP is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
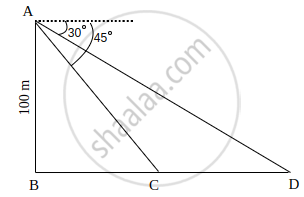
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]