Advertisements
Advertisements
Question
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
Solution
Let AB be the lighthouse and C be the position of the ship from the lighthouse.
Suppose the distance of the ship from the lighthouse be x m.
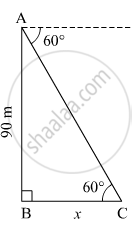
In right ∆ABC,
\[\tan60^\circ = \frac{AB}{BC}\]
\[ \Rightarrow \sqrt{3} = \frac{90}{x}\]
\[ \Rightarrow x = \frac{90}{\sqrt{3}} = 30\sqrt{3}\]
\[ \Rightarrow x = 30 \times 1 . 73 = 51 . 9 m\]
Thus, the ship is 51.9 m away from the lighthouse.
RELATED QUESTIONS
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
A Technician has to repair light on a pole of height 10 m. She needs to reach a point 1 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60∘ to the ground, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder?
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


