Advertisements
Advertisements
प्रश्न
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
विकल्प
True
False
उत्तर
This statement is False.
Explanation:
To understand the fact of this question, consider the following example
I. A tower `2sqrt(3)` m high casts a shadow 2 m long on the ground, then the Sun’s elevation is 60°.
In ΔACB,
tan θ = `"AB"/"BC" = (2sqrt(3))/2`
⇒ tan θ = `sqrt(3)` = tan 60°
∴ θ = 60°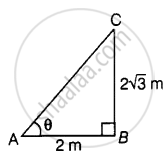
II. A same height of tower casts a shadow 4m more from preceding point, then the Sun’s elevation is 30°.
In ΔAPB,
tan θ = `"AB"/"PB" = "AB"/("PC" + "CB")`
⇒ tan θ = `(2sqrt(3))/(4 + 2) = (2sqrt(3))/6`
⇒ tan θ = `sqrt(3)/3 * sqrt(3)/sqrt(3) = 3/(3sqrt(3)`
⇒ tan θ = `1/sqrt(3)` = tan 30°
∴ θ = 30°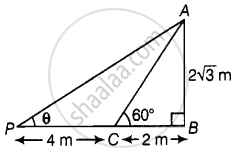
Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is decreasing.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The elevation of a tower at a station A due north of it is α and at a station B due west of A is β. Prove that the height of the tower is `\frac{AB\sin \alpha \sin \beta }{\sqrt{\sin^{2}\alpha -\sin ^{2}\beta `
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
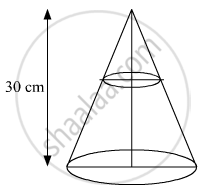
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A kite is flying at a height of 30 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
