Advertisements
Advertisements
प्रश्न
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
उत्तर
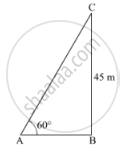
Let C be the position of kite above the ground such that it subtends an angle of 60° at point A on the ground.
Suppose the length of the string, AC be l m.
Given, BC = 45 m and ∠ BAC = 60°.
In ΔABC:
`sin60^@=(BC)/(AC)`
`therefore sqrt3/2=45/l`
`rArrl=(45xx2)/sqrt3=90/sqrt3=30sqrt3`
Thus, the length of the string is`30sqrt3`.
APPEARS IN
संबंधित प्रश्न
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
