Advertisements
Advertisements
Question
Assertion (A): The probability that a leap year has 53 Sundays is `2/7`.
Reason (R): The probability that a non-leap year has 53 Sundays is `1/2`.
Options
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Solution
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
APPEARS IN
RELATED QUESTIONS
The probability of an event is greater than or equal to ______ and less than or equal to ______.
In a simultaneous throw of a pair of dice, find the probability of getting an even number on one and a multiple of 3 on the other
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting the queen of diamonds.
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is a red card
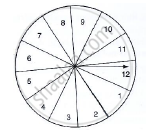
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the number, 1, 2, 3, ..., 12 as shown in Fig. below. What is the probability that it will point to an odd number?
A bag contains 100 identical marble stones which are numbered 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears a perfect square number.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
Six faces of a die are as shown below.

If the die is rolled once, find the probability of - ‘A’ appears on upper face.
A die is rolled twice. Find the probability that 5 will come up both the times.
In a game, the entry fee is Rs 5. The game consists of a tossing a coin 3 times. If one or two heads show, Sweta gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise she will lose. For tossing a coin three times, find the probability that she just gets her entry fee.
