Advertisements
Advertisements
Question
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Solution
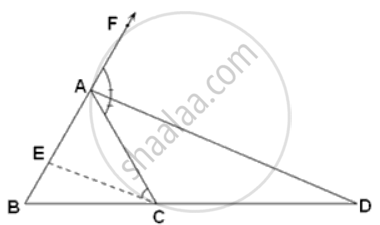
In ΔABC, CE || AD
∴ `"BD"/"CD" = "AB"/"AE"`.....(i)
(By Basic Proportionality theorem)
AD is e bisector of ∠CAF
∠FAD = ∠CAD......(ii)
Since CE || AD
Therefore,
∠ACE = ∠CAD......(iii) ...(alternate angles)
∠AEC = ∠FAD......(iv) ...(corresponding angles)
From (ii) and (iii) and (iv)
∠AEC = ∠ACE
In ΔAEC,
∠AEC = ∠ACE
AC = AE ......(v) ...(Equal angles have equal sides opposite to them)
From (i) and (v)
`"BD"/"CD" = "AB"/"AC"`.
APPEARS IN
RELATED QUESTIONS
In figure, find ∠L

In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

A ship is 400m laig and 100m wide. The length of its model is 20 cm. find the surface area of the deck of the model.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The length of a scale in km represented by 1cm on the map.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
Check whether the triangles are similar and find the value of x
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?

In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
