Advertisements
Advertisements
Question
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
Solution
Scale = 1:20000
1km = 100000cm
4km = 400000cm
`"distance(map)"/"distance(land)"` = Scale
`"distance(land)"/(400000)" = (1)/(20000)`
4km distance on map
= `(400000)/(20000)`
= 20cm.
APPEARS IN
RELATED QUESTIONS
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
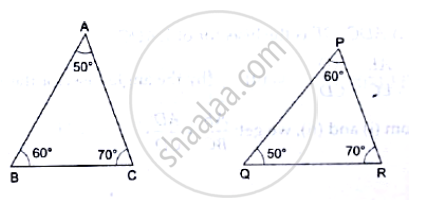
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

In the figure, which of the following statements is true?
