Advertisements
Advertisements
Question
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

Solution
∠ABC = ∠DAC = x ...(Say)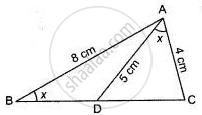
AB = 8 cm,
AC = 4 cm,
AD = 5 cm.
i. In ΔACD and ΔBCA
∠ABC = ∠DAC ...(Given)
∠ACD = ∠BCA ...(Common angles)
`=>` ΔACD ∼ ΔBCA ...(AA criterion for similarity) (i)
Hence ΔACD is similar to ΔBCA.
ii. In ΔACD and ΔBCA
ΔACD ∼ ΔBCA ...[From (i)]
`(AC)/(BC) = (CD)/(CA) = (AD)/(BA)`
`=> (4)/(BC) = (CD)/(4) = (5)/(8)`
`=> (4)/(BC) = (5)/(8)`
`=> BC = (8 xx 4)/(5) = (32)/(5)`
= 6.4 cm
And `(CD)/(4) = (5)/(8)`
`=> CD = (5 xx 4)/(8)`
`=>` CD = 2.5 cm
iii. In ΔACD and ΔBCA
ΔACD ∼ ΔBCA ...[From (i)]
`"Area of ΔACD"/"Area of ΔABC" = ("AC"/"AB")^2`
`=> "Area of ΔACD"/"Area of ΔABC" = 4^2/8^2 = 16/64 = 1/4`
RELATED QUESTIONS
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The areas of two similar triangles are `81cm^2` and `49cm^2` respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
The areas of two similar triangles are `64cm^2` and `100cm^2` respectively. If a median of the smaller triangle is 5.6cm, find the corresponding median of the other.
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
Which of the following is not a test of similarity?
