Advertisements
Advertisements
Question
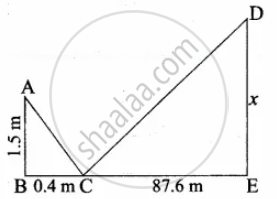
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
Solution
Let the height of the tower ED be “x” m.
In ∆ABC and ∆EDC.
∠ABC = ∠CED = 90° ...(vertical Pole)
∠ACB = ∠ECD ...(Laws of reflection)
∆ABC ~ ∆DEC
`"AB"/"DE" = "BC"/"EC"`
`1.5/x = 0.4/87.6`
x = `(1.5 xx 87.6)/(0.4)`
= `(1.5 xx 876)/4`
= 1.5 × 219
= 328.5
The height of the Lamp Post = 328.5 m
APPEARS IN
RELATED QUESTIONS
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
In Δ ABC , MN || BC .

If `"AB"/"AM" = 9/4` , find `("Ar" ("trapezium MBCN"))/("Ar" . (triangle "ABC"))`
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

