Advertisements
Advertisements
प्रश्न
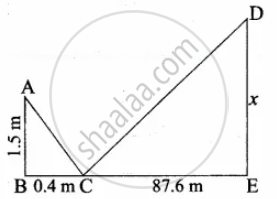
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
उत्तर
Let the height of the tower ED be “x” m.
In ∆ABC and ∆EDC.
∠ABC = ∠CED = 90° ...(vertical Pole)
∠ACB = ∠ECD ...(Laws of reflection)
∆ABC ~ ∆DEC
`"AB"/"DE" = "BC"/"EC"`
`1.5/x = 0.4/87.6`
x = `(1.5 xx 87.6)/(0.4)`
= `(1.5 xx 876)/4`
= 1.5 × 219
= 328.5
The height of the Lamp Post = 328.5 m
APPEARS IN
संबंधित प्रश्न
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

Are the triangles in the given figure similar? If yes, by which test?

On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
In the figure, which of the following statements is true?
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF
In ΔPQR, S and T are points on PQ and PR respectively. `(PS)/(SQ) = (PT)/(TR)` and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
