Advertisements
Advertisements
प्रश्न
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
पर्याय
∠B = ∠E
∠A = ∠D
∠B = ∠D
∠A = ∠F
उत्तर
∠B = ∠D
Explanation;
Hint: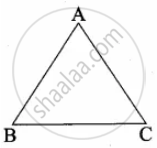
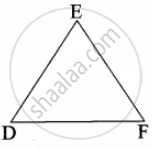
`"AB"/"ED" = "BC"/"DF" = "AC"/"EF"`
∴ ∠B = ∠D
APPEARS IN
संबंधित प्रश्न
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Given is a triangle with sides 3 cm, 5 cm and 6 cm. Find the sides of a triangle which is similar to the given triangle and its shortest side is 4.5 cm.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
