Question

 

 

In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD² = 7 AB²

 

 

Answer 1

 

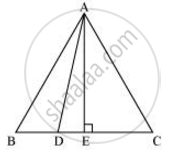
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.

`∴ BE = EC = (BC)/2 = a/2`

And, AE = `(asqrt3)/2`

Given that, BD = `1/3BC`

∴ BD = a/3

`DE = BE - BD = a/2 - a/3 = a/6`

Applying Pythagoras theorem in ΔADE, we get

AD² = AE² + DE²

`AD^2 = ((asqrt3)/2)^2 + (a/6)^2`

`= ((3a^2)/4) + (a^2/36)`

`= (28a^2)/36`

`= 7/9 AB^2`

⇒ 9 AD² = 7 AB²